Recent revelations from Cambridge Analytica and the Trump campaign show how vulnerable our privacy is to innocuous apps installed by our friends. In an new preprint, we model how our privacy is impacted by the people we interact with. Our findings show that node-based intrusions, attacks on our privacy through our friends, is becoming one of the main privacy risk in today’s networked societies.
In the span of a week, Cambridge Analytica turned from yet another Big Data analytics company to being in the media spotlight and the focus of attention from regulators. The reason for such a sudden interest? A whistleblower’s revelations that the company obtained private data on 30 to 50 million Americans, and used this information to assist the Trump campaign through a large scale, micro-targeted, Facebook ad campaign.
All of this started in 2014 when a Cambridge University researcher, Aleksandr Kogan, developed a personality test app, that, in addition to collecting your own personal data, collected data about your friends. This app was installed by over 270,000 unsuspecting Americans (some of whom were recruited through MTurk). While the users gave “informed consent” for the app to collect the data, few of them realized that the app would harvest information not only about themselves, but also about their entire social circle. This data was then acquired by Cambridge Analytica to help the Trump campaign analyze people’s political preferences.
These revelations have come as a shock to many. Besides the concerns of large-scale manipulation, few realized how easy it had been for Kogan to harvest their data. The fact that your friend’s farming simulation game might be actively spying on you is an unsettling fact that most of us were completely unaware of.
This risk to your privacy, incurred by the privacy choice of those you interact with (as well as Facebook’s settings), is what we call group privacy. We are convinced that group privacy, attacks on your privacy through your friends, is becoming one of the main privacy risk in today’s networked societies. Our latest research on this topic is currently under review but, given the recent revelations, we felt it was important for our results to be available to the public. We posted today the preprint of our manuscript, “Quantifying Surveillance in the Networked Age: Node-based Intrusions and Group Privacy”, on arXiv.
In Quantifying Surveillance in the Networked Age, we investigate and quantify how the privacy settings of the people we interact with affect our privacy. We consider various contexts where people interact with one another along a network: all the people we friended on Facebook, the people around us on the street, or the people we call and text on our phone. More precisely, we model the risk of node-based intrusions: if an attacker compromise some nodes (people, phones, etc) in the network, e.g. through a Facebook or smartphone app, how does it impact everyone else’s privacy? How many people’s data does he have access to and is the fact that we live in an increasingly connected society (where we connected to anyone else on earth by only six degrees of separation making the matter worse?
To answer those questions and quantify the reach of the Cambridge Analytica leak, we introduced the concept of node-observability, the number of people (fraction of the nodes in the graph) that are observed when I compromised nodes in the graph. Using this notion, we were able to independently confirm that Cambridge Analytica was likely to have collected data about 46.6M Americans and that the Obama 2012 campaign had likely access to data about 102M Americans (his campaign staff reported to have “ingested the entire U.S. social graph”. We then showed that similar attacks are likely to happen in other settings e.g. using smartphone apps to collect location data. Group privacy, distributed attacks on our privacy through our friends, are much more likely than previously believed and, in our opinion, one of the main privacy risk moving forward.
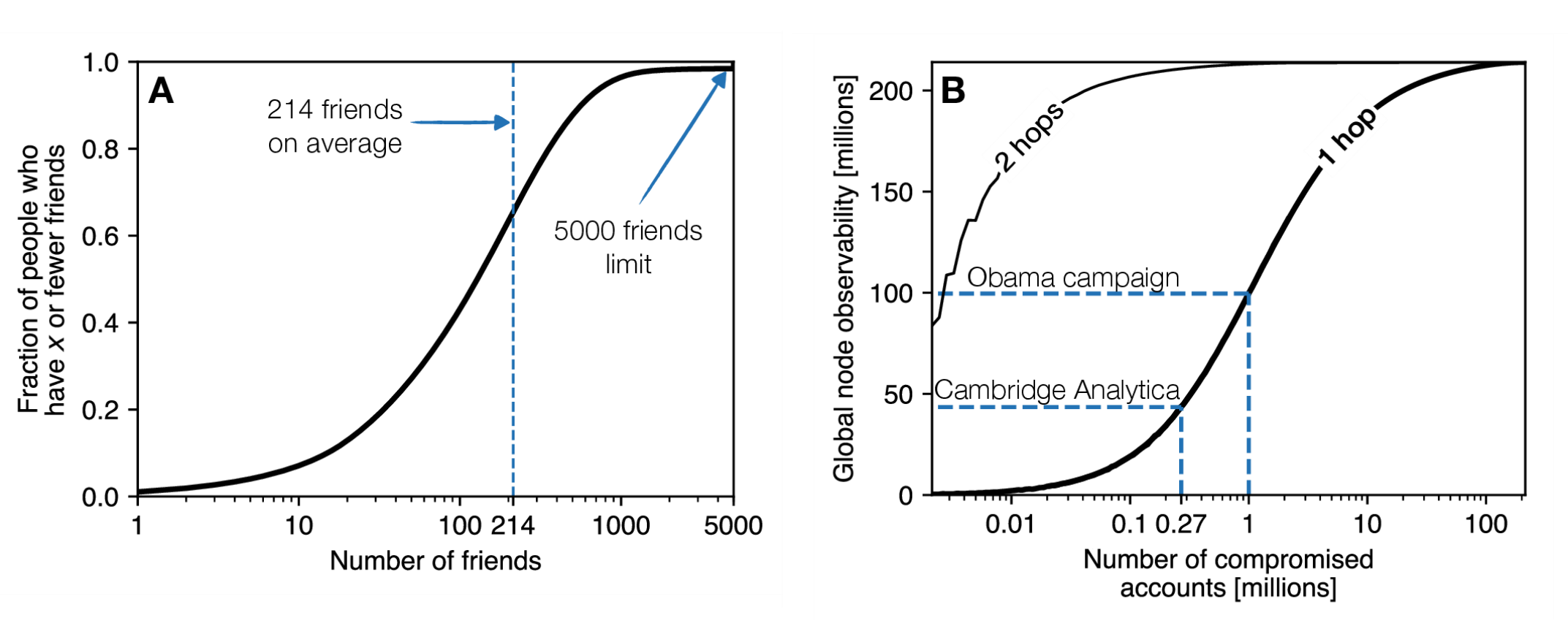
In the paper, we first prove that all we need to estimate the 1-hop node-observability, the number of profiles I can access if 10.000 people install my app, is the degree distribution of the graph: how many users there are on Facebook, and how many friends they have. We extracted the former (214M) from Statistica and the latter from a paper published by FB researchers. The degree distribution (Fig. 1) shows that, in 2011, people on FB had 214 friends on average and couldn’t have more 5000 friends.
Using these two pieces of information, our model allows us to estimate Facebook’s node-observability, the number of profiles that are accessible if 10 000, 100 000 or 1M people install an app like Kogan’s. Qz reported that 270 000 installed Kogan’s app allowing him and the Trump campaign to access the profiles of 30M to 50M Americans. Knowing only the number of people who install the app, our model allows us to independently validate that the Trump campaign had likely access to the profile of 46.6M Americans which they then used to target voters (Fig. 1).
The Trump campaign was not the first one to realize the power of social media. In fact, the Obama campaign relied on a similar, albeit much more transparent, mechanism in 2012. The Washington Post reported that roughly 1M people installed their Obama 2012 Facebook app allowing them, according to our model, to use data about 100M Americans to recommend to app users who they should reach out to (Fig. 1). This contrast with claims from his staff at time who said they had “ingested the entire U.S. social graph”
The fact that Kogan was able to extract so much data with Facebook having no actual technical control over the information is what lead some to call it a data breach. Indeed, as Jason Koebler said to Motherboard: “If your data has already been taken, Facebook has no mechanism and no power to make people delete it.. If your data was taken, it has very likely been sold, laundered, and put back into Facebook”. Furthermore, research (incl. ours) showed that big data cannot - be - effectively - anonymized.
While our analysis shows that both the Trump and Obama campaign use modern privacy’s network effects to gain access to data about millions of Americans, it could have been even worse. Facebook, at the time of the Cambridge Analytica data collection, only let apps access data from your friends (what we call 1-hop). Their previous privacy settings were a lot more loose, letting you share data with friends of friends (2-hops). While this may sound like a small difference, it is not. Our analysis shows that such settings would have allowed Cambridge Analytica to collect a striking 210M profiles, 98.5% of the US Facebook population!
If you have been following the surveillance debate, this might not be the first time you are hearing about “hops”. A similar idea has indeed been built into US regulation allowing intelligence agencies not only to collect phone records of suspects, but also to collect the phone records of their contacts (1 hop), or the contacts of their contacts (2 hops). Until the Snowden revelations, even 3-hop contacts could be collected. Using our metric and a real-world large-scale mobile phone dataset, we showed that all it would take to observe 86.6% of all communications occuring in the US through this 3-hops policy is to convince a judge that 0.01% of the nodes are “suspicious”. Under the new, 2-hops, policy this would still allow an attacker to observe 18.6% of all the communication.
Node-observability attacks apply beyond social networks and can, for example, be used to collect large-scale location data through the phone of people around you. The culprit here is a tiny, convenient, feature of your phone that you probably have never really thought about: your phone will automatically connect to Wi-Fi networks you have connected to before. To be more precise, your phone will attempt to connect to Wi-Fi that have the same name as Wi-Fi you have connected to before (and will connect to them if the original Wi-Fi was not encrypted). Using this, I would first embed a piece of code in a couple of apps on the Play or App store, like what UK startup Tamoco is already doing. Then, I would have the app create fake hotspots with popular names (xfinity-wifi, etc), allowing me to record the identifier of phones who connect to my hotspot and the GPS position of the phone. Using a real mobility dataset, we show this attack to be highly effective: compromising as few as 1% of the phones in London (Tamoco reports to have their code installed on 12M people’s phone in the UK) would allow an attacker to track the location (in 1km²) of about 54% of the city’s population.
In our modern networked societies, privacy is a shared responsibility. The people we interact with, be it at home, at work, or on the streets, impact our privacy. In our paper, we call this group privacy, and we study it through node-based intrusions. Our results show that the privacy risks incurred by the (poor) privacy settings of the people around us are much more important than previously believed, and that network effects makes us highly vulnerable to node-based intrusions compromising even a small fraction of the network. The Cambridge Analytica story is one of the first large scale examples of such group privacy attacks, and it is unlikely to be the last.
Methodology
We extracted the distribution of degrees for the United States Facebook graph from this paper.
Proposition 3.3 from our paper shows that we can compute 1-hop global node-observability using only the list of degrees from the graph, through an expression of the type (for a graph $(V,E), n=|V|$ and $n_c$ compromised nodes): $\rho_v^* = \frac{n_c}{n}+ \frac{n-n_c}{n} \cdot \sum_{v \in V} f\left(degree(v)\right)$. We have the probabilistic distribution $T_D$, and if we assume that nodes are sampled from it independently (by definition of $T_D$), then we compute global node observability as: $\rho_v^* = \sum_{d=1}^n T_D(d) f(d) = {E}(f(D))$
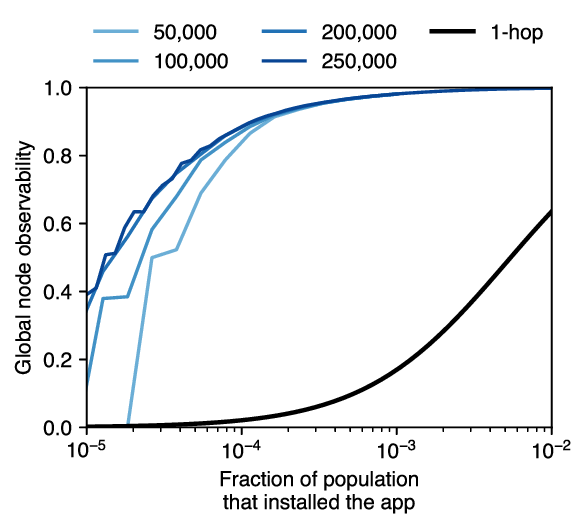
For the 2-hop global node-observability, we sample a graph with a large number of nodes that follows the same distribution as Facebook’s graph, using the configuration model. We studied how the number of nodes influences the observability (Fig. 2), and conclude that taking $N = 250,000$ nodes provides stable enough results to extend to 214 millions (Fig. 2). We then compute 2-hop global node-observability using the code from our paper, which will be made available on publication.